- 全部分类/
- 数理化/
- 数理天地(高中版)
 扫码免费借阅
扫码免费借阅
目录
快速导航-
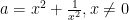
基础精讲 | 依托零点场景,确定参数技法
基础精讲 | 依托零点场景,确定参数技法
-
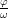
基础精讲 | 三角函数图象变换方法探讨
基础精讲 | 三角函数图象变换方法探讨
-
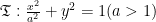
基础精讲 | 曲线系方程在解答解析几何问题中的运用
基础精讲 | 曲线系方程在解答解析几何问题中的运用
-
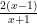
基础精讲 | 证明不等式恒成立的三种方法分析
基础精讲 | 证明不等式恒成立的三种方法分析
-
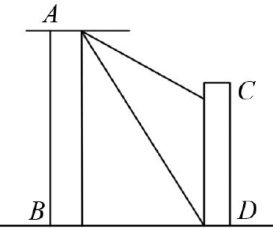
基础精讲 | 高中数学三角函数解题策略及实践应用
基础精讲 | 高中数学三角函数解题策略及实践应用
-
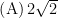
基础精讲 | 圆锥曲线中弦长问题的分类与解题思路
基础精讲 | 圆锥曲线中弦长问题的分类与解题思路
-
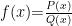
基础精讲 | 换元法在函数值域问题中的应用
基础精讲 | 换元法在函数值域问题中的应用
-
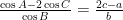
基础精讲 | 正余弦定理在解三角形中的应用
基础精讲 | 正余弦定理在解三角形中的应用
-
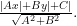
基础精讲 | 浅析如何提高学生的数学解题能力
基础精讲 | 浅析如何提高学生的数学解题能力
-
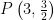
例题精讲 | 新高考下圆锥曲线复习课教学实践与思考
例题精讲 | 新高考下圆锥曲线复习课教学实践与思考
-
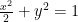
例题精讲 | 关于一个椭圆焦点弦问题的感想
例题精讲 | 关于一个椭圆焦点弦问题的感想
-
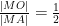
例题精讲 | 一道经典圆锥曲线大题的解题历程
例题精讲 | 一道经典圆锥曲线大题的解题历程
-
例题精讲 | 关于数值大小比较问题的解法举例
例题精讲 | 关于数值大小比较问题的解法举例
-
例题精讲 | 例析高中数学数列通项公式的常见求解方法
例题精讲 | 例析高中数学数列通项公式的常见求解方法
-
例题精讲 | 导数在高中数学解题中的应用
例题精讲 | 导数在高中数学解题中的应用
-
例题精讲 | 深度学习视角下的高中数学解题策略研究
例题精讲 | 深度学习视角下的高中数学解题策略研究
-
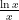
例题精讲 | 恒成立问题的处理方略
例题精讲 | 恒成立问题的处理方略
-
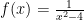
解题技巧 | 学会抓住本质,探寻解题规律
解题技巧 | 学会抓住本质,探寻解题规律
-
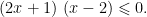
解题技巧 | 高中数学中不等式解法探究
解题技巧 | 高中数学中不等式解法探究
-
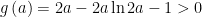
解题技巧 | 含参不等式恒成立数学解题技巧
解题技巧 | 含参不等式恒成立数学解题技巧
-
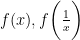
解题技巧 | 常见函数解析式的求解方法分析
解题技巧 | 常见函数解析式的求解方法分析
-
解题技巧 | 抽象函数问题的常规解法例析
解题技巧 | 抽象函数问题的常规解法例析
-
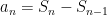
解题技巧 | 探究高中数学开放性试题的解题方法
解题技巧 | 探究高中数学开放性试题的解题方法
-
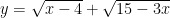
解题技巧 | 变量代换法在高中数学解题中的实践运用
解题技巧 | 变量代换法在高中数学解题中的实践运用
-
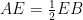
解题技巧 | 平面向量数量积问题的常规解法分析
解题技巧 | 平面向量数量积问题的常规解法分析
-
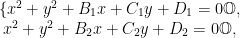
解题技巧 | 解析几何中圆的公切线方程解题思路和技巧分析
解题技巧 | 解析几何中圆的公切线方程解题思路和技巧分析
-
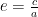
解题技巧 | 求解离心率的常用方法分析
解题技巧 | 求解离心率的常用方法分析
-
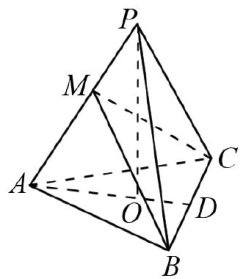
解题技巧 | 巧用向量法求解几类立体几何问题
解题技巧 | 巧用向量法求解几类立体几何问题
-

解题技巧 | 三角函数解题技巧的系统总结与应用分析
解题技巧 | 三角函数解题技巧的系统总结与应用分析
-
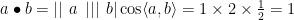
高考高分之路 | 核心素养导向下的平面向量高考备考复习建议
高考高分之路 | 核心素养导向下的平面向量高考备考复习建议
-
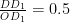
高考高分之路 | 以数学文化为背景的高考试题研究
高考高分之路 | 以数学文化为背景的高考试题研究
-
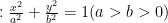
高考高分之路 | 妙用仿射变换,化椭圆为圆
高考高分之路 | 妙用仿射变换,化椭圆为圆
-
高考高分之路 | 新高考视角下高中数学教学面临的困境及方法分析
高考高分之路 | 新高考视角下高中数学教学面临的困境及方法分析
-
优化课堂方法 | 创设情境,培养思维
优化课堂方法 | 创设情境,培养思维
-
优化课堂方法 | 任务驱动下的高中数学问题链教学探究
优化课堂方法 | 任务驱动下的高中数学问题链教学探究
-
优化课堂方法 | 差异化教学在数学课堂中的应用及有效性分析
优化课堂方法 | 差异化教学在数学课堂中的应用及有效性分析
-
优化课堂方法 | 问题探究式教学在高中数学课堂中的应用研究
优化课堂方法 | 问题探究式教学在高中数学课堂中的应用研究
-
优化课堂方法 | 情境教学在高中数学课堂教学中实践的具体策略
优化课堂方法 | 情境教学在高中数学课堂教学中实践的具体策略
-
优化课堂方法 | 高中数学立体几何大单元教学策略的有效性分析
优化课堂方法 | 高中数学立体几何大单元教学策略的有效性分析
-
优化课堂方法 | 基于启发式教学的圆锥曲线数学课堂构建
优化课堂方法 | 基于启发式教学的圆锥曲线数学课堂构建
-
优化课堂方法 | 以多元导入方法激活高中数学课堂教学
优化课堂方法 | 以多元导入方法激活高中数学课堂教学
-
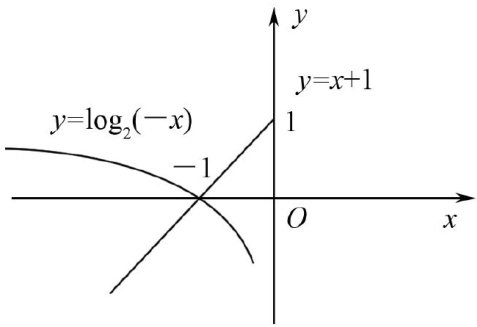
教学思想实践 | 数形结合思想在高中数学教学中的应用研究
教学思想实践 | 数形结合思想在高中数学教学中的应用研究
-
教学思想实践 | 深度学习理论下高中数学“金课"构建路径
教学思想实践 | 深度学习理论下高中数学“金课"构建路径
-
教学思想实践 | 数学建模融入高中数学的教学方法研究
教学思想实践 | 数学建模融入高中数学的教学方法研究
-
教学思想实践 | 基于学科融合的高中数学教学模式研究
教学思想实践 | 基于学科融合的高中数学教学模式研究
-
教学思想实践 | 合作学习在高中数学教育中的理论基础
教学思想实践 | 合作学习在高中数学教育中的理论基础
-
教学思想实践 | 基于核心素养的高中数学分层教学
教学思想实践 | 基于核心素养的高中数学分层教学
-
教学思想实践 | 核心素养视域下数形结合在高中数学教学中的应用
教学思想实践 | 核心素养视域下数形结合在高中数学教学中的应用
-
教学经验交流 | 指向高阶思维能力的高中数学教学策略
教学经验交流 | 指向高阶思维能力的高中数学教学策略
-
教学经验交流 | 基于核心素养的高中数学单元解题教学实践与反思
教学经验交流 | 基于核心素养的高中数学单元解题教学实践与反思
-
教学经验交流 | “双减”对高中数学教学效率提升的影响及对策
教学经验交流 | “双减”对高中数学教学效率提升的影响及对策
-

教学经验交流 | 高中数学函数相关习题的解题分析
教学经验交流 | 高中数学函数相关习题的解题分析
-
教学经验交流 | 数学史融入高中数学课堂教学的路径研究
教学经验交流 | 数学史融入高中数学课堂教学的路径研究
-
教学经验交流 | 高中数学作业优化设计
教学经验交流 | 高中数学作业优化设计
-
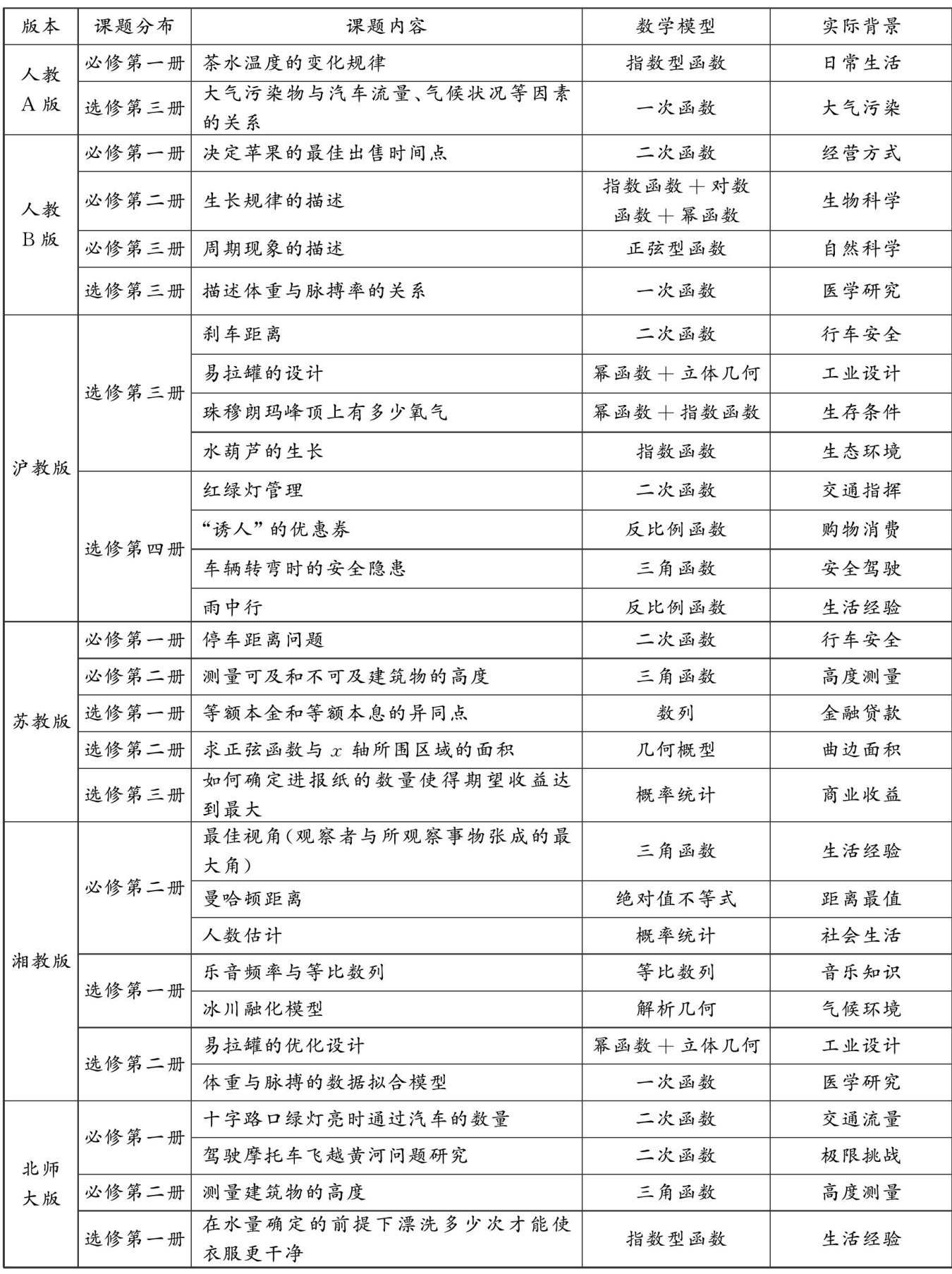
教学经验交流 | 高中多版教材中数学建模的对比研究
教学经验交流 | 高中多版教材中数学建模的对比研究
-
教学经验交流 | 探析在高中数学教学中融入情感教育
教学经验交流 | 探析在高中数学教学中融入情感教育
-
核心素养培养 | 高中数学核心素养培养策略与实践探究
核心素养培养 | 高中数学核心素养培养策略与实践探究
-
核心素养培养 | 开辟数学核心素养提高的特色途径
核心素养培养 | 开辟数学核心素养提高的特色途径
-
核心素养培养 | “逻辑推理"核心素养培养下高中数学教学研究
核心素养培养 | “逻辑推理"核心素养培养下高中数学教学研究
-
核心素养培养 | 基于核心素养的高中数学大单元教学中数学运算能力的培养
核心素养培养 | 基于核心素养的高中数学大单元教学中数学运算能力的培养
-
核心素养培养 | 高中数学运算素养的学习进阶研究
核心素养培养 | 高中数学运算素养的学习进阶研究
-
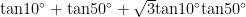
核心素养培养 | 在函数性质教学中培养学生数学核心素养的几点探索
核心素养培养 | 在函数性质教学中培养学生数学核心素养的几点探索
-

学生培养研究 | 量化高中学生数学逻辑推理核心素养水平的模型构建
学生培养研究 | 量化高中学生数学逻辑推理核心素养水平的模型构建
-
学生培养研究 | 逆向思维在高中数学教学中的培养
学生培养研究 | 逆向思维在高中数学教学中的培养
-
学生培养研究 | 高中数学问题解决能力培养的理论框架与教学策略研究
学生培养研究 | 高中数学问题解决能力培养的理论框架与教学策略研究
-
学生培养研究 | 高中数学新教材单元整体教学策略与学生创新能力培养
学生培养研究 | 高中数学新教材单元整体教学策略与学生创新能力培养
-
学生培养研究 | 中职数学教学困境与突破:基于学生需求的教学改革研究
学生培养研究 | 中职数学教学困境与突破:基于学生需求的教学改革研究
-
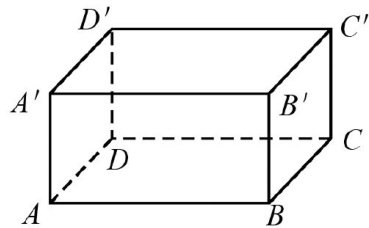
教育技术与数学融合 | “互联网十精准教学"构建高中数学智慧课堂行动研究
教育技术与数学融合 | “互联网十精准教学"构建高中数学智慧课堂行动研究
-
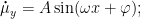
教育技术与数学融合 | 现代信息技术赋能高中数学高效课堂构建的实践探索
教育技术与数学融合 | 现代信息技术赋能高中数学高效课堂构建的实践探索
-
教育技术与数学融合 | 智能时代高中数学互动式校本课程教学平台的构建与应用
教育技术与数学融合 | 智能时代高中数学互动式校本课程教学平台的构建与应用



















 登录
登录