目录
快速导航-
知识篇 | 2025年高考之计数原理考点解读
知识篇 | 2025年高考之计数原理考点解读
-
知识篇 | 2025年高考之成对数据的统计分析备考解读
知识篇 | 2025年高考之成对数据的统计分析备考解读
-

知识篇 | 2025年高考之随机变量及其分布考点解读
知识篇 | 2025年高考之随机变量及其分布考点解读
-
知识篇 | 提升数学应用能力,强化概率统计素养
知识篇 | 提升数学应用能力,强化概率统计素养
-

解题篇 | 巧用赋值法,妙解二项式
解题篇 | 巧用赋值法,妙解二项式
-
解题篇 | 例析隔板法在处理排列组合问题时的应用
解题篇 | 例析隔板法在处理排列组合问题时的应用
计数中的分配或分组问题,一直是排列组合中的一个重点与难点,也是组合应用中的典型问题之一。其中,利用隔板法来处理对应的分配或分组问题,成为高中排列组合的重要方法之一,它主要用于解决相同元素(或具有相同特征或相同地位等)的分配问题。根据问题的创设场景与应用类型,隔板法可分为三种比较常见的题型:① 标准型;②多分型;③少分型。其中后两种题型根据具体的问题场景,加以合理转化与应用,最终都是化为“标准型”来
-

解题篇 | 全概率公式的巧妙应用
解题篇 | 全概率公式的巧妙应用
-
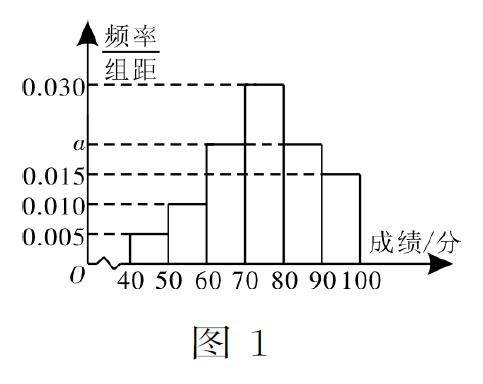
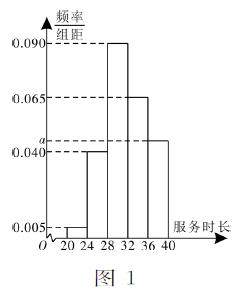
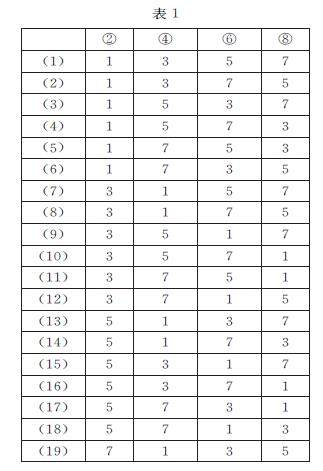
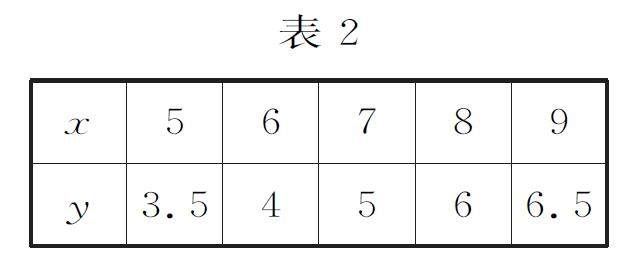
解题篇 | 数据分析,直观想象
解题篇 | 数据分析,直观想象


























 登录
登录